
The mathematician Maurice Karnaugh, has constructed a chart that aids in minimization Boolean functions;
Karnaugh map.
( The Map for Synthesis of Combinational Logic Circuits, AIEE, Nov. 1953 ).
The Karnaugh map exploits the fact that we humans are good at recognizing patterns,
and thus with help of a chart can determine which terms in a Boolean function is to be combined to
give the simplest expression.
The Karnaugh map can conveniently be used for functions of up to four variables,
and with a little practice up to six variables.

The truthtable consists of 11 "1" and 5 "0". According to earlier, we know that the function can be expressed in the SoP form with 11 mintermer or PoS form with 5 maxtermer. Anyone who used the Boolean algebra know that it then follows hard work to produce simpler expressions. Minterms could be combined in many different ways, which all result in different simplified expression - How do we know that we have found the will I know I have found the basest?
Instead of simplifying the function with Boolean algebra, we will here use the method of Karnaugh map.
In the Karnaugh map the logical function's truth table is lined up in a different way. A logic function of four variables has a truth table with 16 rows and these are depicted in a Karnaugh as 16 frames. (The ones/zeros in the Karnaugh map are taken from the truth table). The frames in the Karnaugh map are numbered after the Gray code so that the two "neighbor" frames only differ in one variable.

The frames "5" and "13" are "neighbors" in the Karnaugh map
( but they are distant from each other in the truthtable ).
They correspond to two mintermer with four variables,
and the figure shows how, with Boolean algebra,
they can be reduced to one term with three variables.
What the two frames have in common is that b = 1, c = 0 and d = 1;
and the reduced term expresses just that. (The term is a product of b, d and c's inverse).
Everywhere in the Karnaugh map where one can find two ones that are "neighbors" (vertically or horizontally)
the minterms could be reduced to "what they have in common". This is called a grouping.
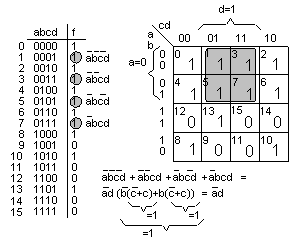
Frames "1" "3" "5" "7" is a group of four frames with "1" that are "neighbors" to each other. Here too, the four minterms could be reduced to a term that expresses what is common for the frames, namely that a = 0 and d = 1. Everywhere in Karnaugh map where one can find such groups of four ones such simplifications can be done, grouping of four.

All groups of 2, 4, 8, (... 2 N ie. powers of 2) frames containing ones can be reduced to a term, with what they have in common, grouping of n.
Karnaugh-torus |  |
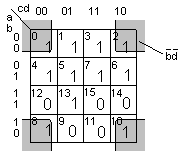
The Karnaugh map should be drawn on a torus (a donut). When we reach an edge, the graph continnues from the opposite side! Frame 0 is the "neighbor" with frame 2, but also the "neighbor" with frame 8 which is "neighbor" to frame 10.
One is looking for the bigest grouping as possible. In the example, there is a grouping with eight ones (frames 0,1,3,2,4,5,7,6).
Corners (0,2,8,10) is a NARROWING of four ones.
Two of the frames (0.10) has already been included in the first group,
but it does not matter if a minterm is included multiple times.
All ones in the logic function must either be in a grouping, or be included as a minterm.
The "1" in frame 13 may form a group with "1" in frame 5,
unfortunately there are no bigger grouping for this "1".
The resulting function is apparently a major simplification compared to the orginal function with the 11 minterms.

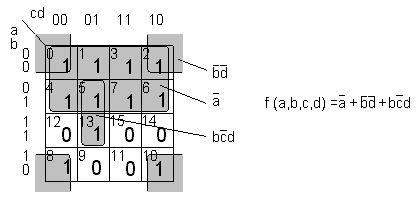
The Karnaugh map is also useful for groupings of 0's. The groupings may include the same number of frames as the case of groupings of 1's. In this example, 0: s are grouped together in pairs with their "neighbors". Maxterms are simplified to what is in common for the frames.
The simplified expression is the product of three sums it represents a very substantial simplification of the original functins's five maxterms.
© William Sandqvist william@kth.se