
All logic functions could be realised with the two gates AND and OR kombined in two levels.
There are logic circuits with more than two levels, but it's not necessary with more than two levels.
We here assume that the input-variables exists both in orginal and in inverted form.
( If the input variables are not available in inverted form,
one of course needs inverters to ).

One can realize the gate circuit directly from the truth table.
If the function should be "1" for a particular variable combination (a, b) for example
(0.1), one can accomplish this by forming the product of a and b's inverse.
This product is only "1" for the combination (0.1).
One such product is called a minterm.
The function can then be expressed as a sum of all such minterms.
Each minterm contributing with a "1" from the truth table.
One says that the function is expressed in SoP-form (Sum of Products).
The logic circuit's minterms are formed with AND gates and these are then summed with an OR gate.
This method to translate a truth table into gates can always be used,
but the solution is not optimal,
there may be a lot simpler circuit with fewer gates that do the same job.
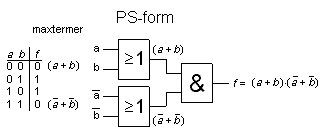
Alternatively, one can focus on the truth table 0's.
If a gate circuit reproduces the function 0's correct then of course to the 1's are right!
Thus, if the function is to be "0" for a particular variable combination (a, b) for example
(0.0) we can form the sum (a + b).
This sum can only be "0" for the combination (0.0).
Such a sum is called a maxterm.
The function is then expressed as a product of all such maxterms.
Each maxterm contributes with a "0" from the truth table.
The function is said to be expressed in PoS Form (Product of Sums).
The logic functin's maxtermer formed with OR gates, and these are then multiplied in an AND gate.
Although this method too is generally useful, it is not optimal.
If the truth table contains many "1" and few "0" the PoS-form is favorable.
If the truth table has few "1" the SoP-form is instead favorable.
Moreover, the is an ability to make simplifications of gate circuit with the Boolean algebra.
Comment: The truth table in this example could not be realized with simpler gate circuits. kan inte realiseras med enklare grindnšt šn de ovan visade. Both PoS-form and SoP-form has the same cost for this example.
A function of two variables have three 1's in the truth table. One may then express this function of SoP-form with three mintermer. This is far from the simplest expression of this function (you may already have recognized that the function is the OR function ?) . With Boolean algebra, the function can be simplified.
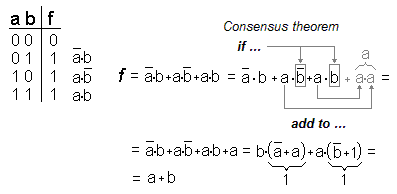
The Consensus theorem means that you may add a term to the function. It may seem "backwards" to add a term when you're looking to simplify the function, but apparently this facilitates the further simplification down to the end result a + b.
This result can also be accessed directly by expressing the truth table's only "0" as a maxterm (a + b).
Another way to reach this result is to lock at the opposite functionen, that has one only "1" for a=0 and b=0. If this function is inverted, and by using de Morgans theorem, we get a+b.
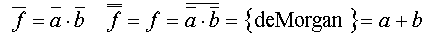
© William Sandqvist william@kth.se