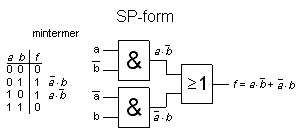
Alla logiska funktioner kan realiseras med hjälp av grindtyperna AND och OR kombinerade i två steg.
Det förekommer grindnät med fler steg än två, men det är inte nödvändigt med fler steg än två.
Vi förutsätter här att ingångsvariablerna även finns i inverterad form.
( Om ingångsvariablerna inte finns att tillgå i inverterad form,
så behöver man naturligtvis även inverterare till detta ).

Man kan realisera grindnätet direkt från sanningstabellen.
En om funktionen ska vara "1" för en viss variabelkombination (a,b) tex.
(0,1) så kan man åstadkomma detta genom att bilda produkten av a:s invers och b.
Den produkten är ju bara "1" för kombinationen (0,1).
En sådan produkt kallas för en minterm.
Funktionen kan sedan uttryckas som en summa av alla sådana mintermer.
Varje minterm bidrar med en etta från sanningstabellen.
Man säger att funktionen är uttryckt på SP-form ( Summa av Produkter ).
Grindnätets mintermer bildas med AND-grindar och dessa summeras med en OR-grind.
Denna metod att översätta en sanningstabell till ett grindnät kan alltid användas,
men lösningen är inte optimal,
det kan finnas mycket enklare grindnät med färre grindar som gör samma arbete.
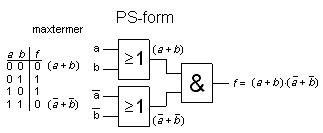
Alternativt kan man inrikta sig på sanningstabellens 0:or.
Om ett grindnät återger funktionens 0:or korrekt så är ju även 1:orna rätt!
Om således funktionen ska vara "0" för en viss variabelkombination (a,b) tex.
(0,0) så bildar man summan ( a + b ).
Den summan kan ju bara bli "0" för kombinationen (0,0).
En sådan summa kallas för en maxterm.
Funktionen uttrycks som en produkt av alla sådana maxtermer.
Varje maxterm bidrar med en 0:a från sanningstabellen.
Funktionen sägs vara uttryckt på PS-form ( Produkt av Summor ).
Grindnätets maxtermer bildas med OR-grindar och dessa multipliceras med varandra med en AND-grind.
Även denna metod är generellt användbar, men inte optimal.
Om sanningstabellen innehåller många ettor och få nollor är PS-formen gynnsam.
Om sanningstabellen har få ettor är i stället SP-formen gynnsam.
Dessutom är i allmänhet möjligheten att göra förenklingar av grindnäten med Boooles algebra stor.
Kommentar: Sanningstabellen i detta exempel kan inte realiseras med enklare grindnät än de ovan visade. PS-formen och SP-formen har i detta fall precis samma kostnad ( i dioder räknat ).
En funktion av två variabler har tre ettor i sanningstabellen. Man kan då uttrycka funktionen på SP-form med tre mintermer. Detta är långt ifrån det enklaste uttrycket för denna funktion ( du kanske redan har känt igen funktionen som OR-funktionen? ). Med Booles algebra kan funktionen förenklas.

Koncensuslagen innebär att man man får lägga till en term till funktionen. Det kan verka "bakvänt" att lägga till en term när man är ute efter att förenkla funktionen, men som synes så underlättar detta den vidare förenklingen ner till slutresultatet a+b.
Slutresultatet kan man också nå direkt genom att uttrycka sanningstabellens enda nolla som en maxterm ( a + b ).
Slutresultatet kan också nås genom att man tittar på den motsatta funktionen, den som har en ensam etta för a=0 och b=0. Om den ( motsatta ) funktionen inverteras med hjälp av de Morgans lag får man a+b.
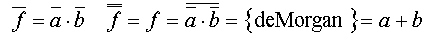
© William Sandqvist william@kth.se