
Detta är ditt eget unika frågehäfte.
Normalt kräver systemet siffersvar,
så därför innehåller frågehäftet JAVA-script som räknar fram siffersvar när svaren avges på annat sätt.
Till frågehäftet hör ett svarsformulär med samma nummer. Med det provar Du siffersvaren, och får reda på om Du svarat rätt eller fel på frågorna i frågehäftet.
Du kan svara hur många gånger som helst, men skriv upp alla dina rätta svar.
Svarsrutan försvinner när Du svarar rätt.
Uppgifterna behöver inte besvaras i någon speciell ordning.
Vid eventuella tekniska problem skickar Du i stället in svaren i ett mail till examinator för manuell registrering.
| Namn: | |
|---|---|
| Personnummer: | |

Mycket nöje och lycka till!
I reglertekniken kommer Du ofta behöva bestämma rötter till polynom.
Polynom med högre gradtal är inte så roliga att lösa med bara papper och penna.
Inom reglertekniken är det mest använda datorprogrammet Matlab så passa nu på att bekanta dig med det programmet!
Beräkna rötterna till följande tredjegradspolynom:
y = 3,2x3 - 1,3x2 - 50x + 56
Tips! Använd programmet Matlab.
Du ska svara med rötterna sorterade i följande ordning, efter stigande argument, och vid samma argument efter ökande belopp. För reella rötter måste Du svara med att imaginärdelen är 0, det går inte att lämna någon svarsruta tom.
| Rot 1 | Rot 2 | Rot 3 | |||
|---|---|---|---|---|---|
| Re | Im | Re | Im | Re | Im |
Du kan föra in Dina siffervärden i tabellen nedan för att kunna ha dem till hands senare:
|
|
|
Svar d) |
|||||||||||||||
| | ||||||||||||||||||
I reglertekniken behöver man ibland partialbråksuppdela
produktuttryck till summor som är enklare att behandla.
Laplacetabeller är så begränsade
att komplicerade uttryck först måste partialbråksuppdelas
innan man kan hitta de motsvarande transformerna i tabellen.
Partialbråksuppdela följande uttryck. Bestäm konstanterna a b och c så att höger led blir lika med vänster led av ekvationen.

Tips! Matlab-kommandot residue() kan vara användbart.
Du kan föra in Dina siffervärden i tabellen nedan för att kunna ha dem till hands senare:
| Svar a) a = ? | Svar b) b = ? | Svar c) c = ? |
| |

Förenkla överföringsfunktionen GTOT=C/R till ett enda block med hjälp av reduktionsreglerna för blockschemor.
Välj rätt uttryck för nämnare och täljare med hjälp av listboxarna. Klicka sedan på Calculate för att beräkna din svarskod.

|
 |
Skriv upp ditt siffervärde för att kunna ha det till hands senare:
| Svar a) GTOT | |
|---|---|
| Svarskod | |

Nedan visas hur det typiska stegsvaren från sex olika processer ser ut. Du ska para ihop stegsvaren med rätt processöverföringsfunktion.


a) Para ihop stegsvaren a-f med processernas överföringsfunktioner 1-5. Svara med siffrorna packade som ett sexsiffrigt heltal.
| a | b | c | d | e | f |
|---|---|---|---|---|---|
Du kan föra in Dina siffervärden i tabellen nedan för att kunna ha dem till hands senare:
| Svar a)
(6 siffror packade som ett heltal) |
| |
Systemidentifiering brukar ske med hjälp av avancerade och ofta "dyra" programvaror.
Läroboken ger dock några exempel på enkla diagrammetoder som kan användas för systemidentifiering av några vanligt förekommande processer.
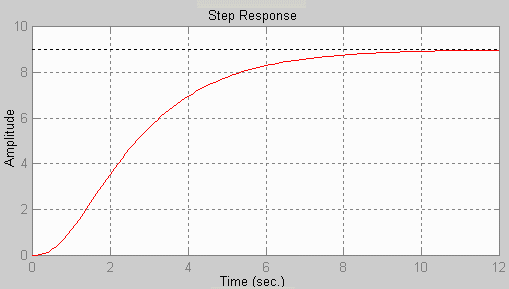
Figuren visar stegsvaret för ett "enhetssteg" från en process som man vet har tre tidkonstanter.
Använd lärobokens diagrammetod för att identifiera processen.
När Du läser av tiderna i figuren ska Du avrunda dem till närmaste 0,25 sek.
Beräkna parametern Q.
OBSERVERA! Det går förmodligen inte att läsa av a
och P, med tillräcklig noggrannhet för de fortsatta beräkningarna i uppgiften,
med lärobokens diagram!

Lärobokens diagram finns "inläst" i tabellform som ett Matlab-script.
[a,P]=aP(Q,n)  aP.m
aP.m
Ladda ner scriptet ( aP.m ) och placera det i Matlabs "arbetsmapp". Om Du tar fram dina värden på a och P med hjälp av detta så blir dina siffror tillräckligt noggranna!
En process med tre (n=3) tidkonstanter har överföringsfunktionen:

a) Uppskatta K [ggr] ur stegsvarsfiguren.
b) Beräkna tidkonstanten T [s].
c) Beräkna tidkonstanten aT [s].
d) Beräkna tidkonstanten a2T [s].
Du kan föra in Dina siffervärden i tabellen nedan för att kunna ha dem till hands senare:
| Svar a) K [ggr] | Svar b) T [s] | Svar c) aT [s] | Svar d) a2T [s] |
| |
|
|
|
Slut på kunskapstestet!