 complex.pdf
complex.pdfEtt vanligt, reellt tal a brukar man åskådliggöra som en punkt på den s.k. tallinjen. Talets storlek representeras av avståndet från punkten ifråga till tallinjens nollpunkt.
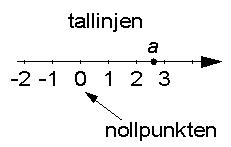
Ett komplext tal z består av två komponenter. Det kan
skrivas a+
Varje komplext tal kan åskådliggöras som en punkt i ett tvådimensionellt koordinatsystem, det komplexa talplanet.
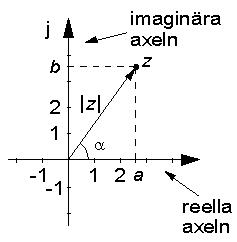
Talet z representeras av en punkt med koordinaterna a och b.
Avståndet från talpunkten till
origo representerar talets belopp eller
talvärde
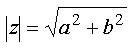
eller generellt
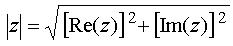
Vinkeln α kallas argumentet för z,
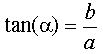
Generellt gäller
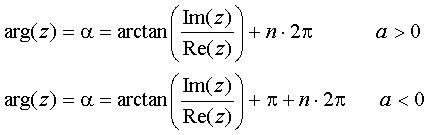
Vi kan också uttrycka z i polär form, dvs i
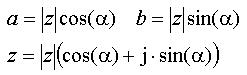
Man kan då tänka sig att det är förbindelselinjen mellan
talpunkten och origo som representerar talet. Vi kan se denna som
en visare med längden
Komplexa tal kan behandlas algebraiskt, varvid följande regler gäller.
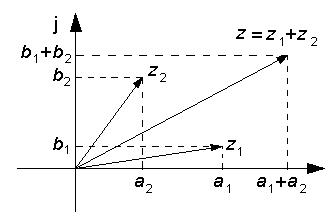
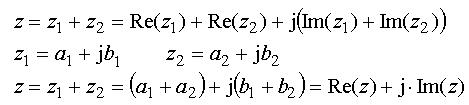
Figuren visar vad additionen innebär i det komplexatalplanet. Visaren för z blir
lika med den geometriska summan av visarna för
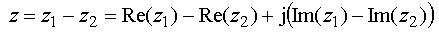
I talplanet blir visaren för z lika med den geometriska
skillnaden mellan visarna för
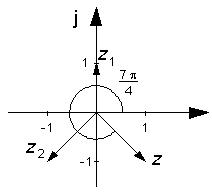
Multiplikationsregeln demonstrerar vi enklast med ett exempel.
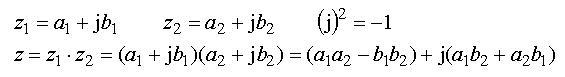
Multiplikationen kan också genomföras med talen uttryckta i polär form.
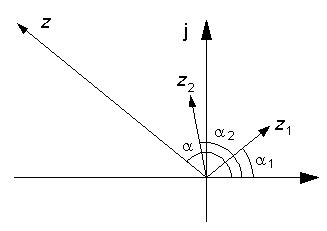
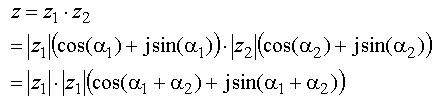
Detta innebär att
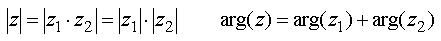
Algebraiskt genomförs divisionen så här:
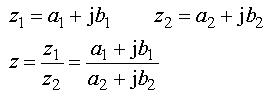
Nu vill man ofta ha resultatet i formen a+
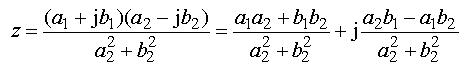
Uttrycks talen i polär form kommer divisionsregeln att se ut så här:
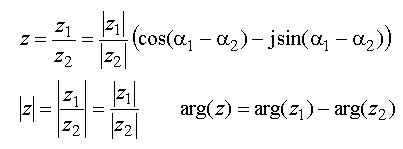
Om z =
( endast om
När man skall bilda beloppet av en produkt eller en kvot
mellan två komplexa tal
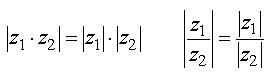
Gör om uttrycket 2 + 3/j till formen a+
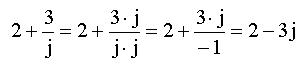
Skriv uttrycket z = 6 +
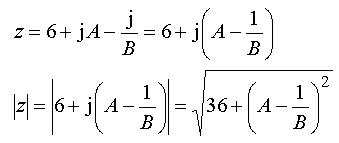
Bestäm
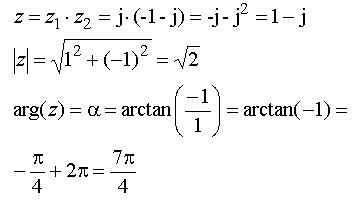
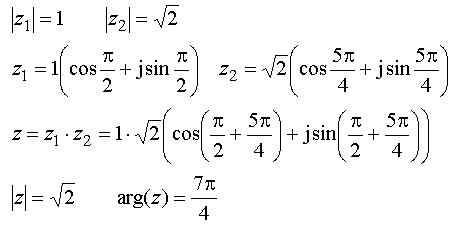
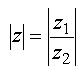
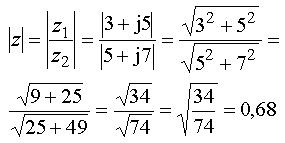
Om man istället hade multiplicerat med konjugatkvantiteten hade man fått
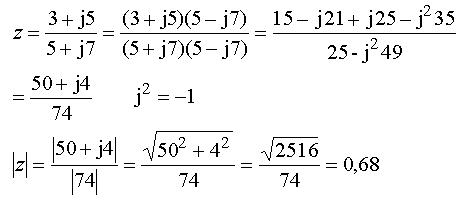
Om man jämför med ovanstående ser man att komplexkonjugeringen medför mycket mera arbete!
Åt vilket håll pekar visaren z = -2 + j2 ?
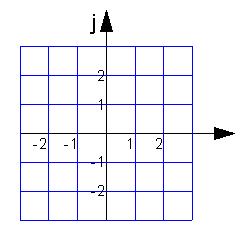
[ Svar ]
Vad är summan av
[ Svar ]
Hur lång är visaren 3 + j4 ?
[ Svar ]
Rita visaren z =

[ Svar ]
Hur stor blir
[ Svar ]
Hur stor blir
[ Svar ]
Vad blir
[ Svar ]
Bestäm

[ Svar ]
Vad blir z =

[ Svar ]
Vad är
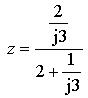
[ Svar ]
Beräkna z.
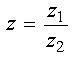

Detta övningshäfte har jag fått av Per-Erik Lindahl. Det har använts som introduktion till växelströmsberäkningar i ellära.
© William Sandqvist william@kth.se